«Քորոնա» Ժահրի Ընթացքին Թուաբանական Պատկերումը Եւ Նախատեսումներ

ԴՈԿՏ. ՀՐԱՉ ՊԱՐՍՈՒՄԵԱՆ

Պատմական.- Միջին դարերուն յետամնաց եւ խոնաւ Եւրոպայի մէջ տեղի ունեցած են ահաւոր համաճարակներ: Առաջին ուսումնասիրութիւնը լոյս տեսած է 17-րդ դարուն, երբ սկսաւ զարգանալ ակադեմական բժշկութիւնը:  Համաճարակի զարգացման թուաբանական վերլուծումը, սակայն, կարելի եղաւ միայն տարբերական համարողութեան (differential calculus) գիւտէն ետք (1): Այս ուղղութեամբ հիմնադրական աշխատանքը կը պատկանի բժիշկ Տանիէլ Պերնուլլիի (1700-1782), որ իր դրոյթով կարողացած էր նախատեսել ծաղկախտ համաճարակի զարգացումը: Տանիէլ Պերնուլլի միաժամանակ հայրն է հեղուկներու մեքանիքի արդի տեսութեան (Fluid Dynamics): Այդ տեսութիւնն է, որ կը բացատրէ, օրինակ,  օդանաւերու թեւերուն ստացած դէպի վեր մղումը, եւ` ոչ միայն (2):

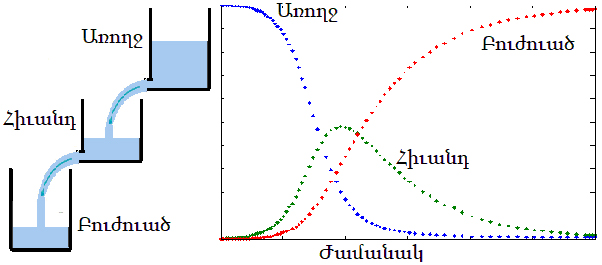Գայլեր եւ ոչխարներ.- Բնական կարգ մը երեւոյթներ կարելի է նկարագրել, այսպէս կոչուած, «Բաժանումային կաղապարում»-ի (Compartmental Modeling) միջոցով: Շատ հասկնալի օրինակ մըն է գծանկարին մէջ ցոյց տրուած հեղուկի հոսքը: Պարզ է, որ բարձր «բաժանումի» հեղուկը ի վերջոյ պիտի լեցուի ստորին բաժանումին մէջ: Նկատի առնուելիք կէտը այն է, որ միջին բաժանումին մէջ հեղուկի մակարդակը նախ որոշ չափով կը բարձրանայ եւ ապա կ՛իջնէ զերոյի: Այդ կը համապատասխանէ բուժելի համաճարակի մը, որ պիտի վարակէ ամբողջ ընկերութիւնը եւ ապա փարատի: Տրուած օրինակը ի հարկէ իրապաշտ չէ, բայց ցոյց կու տայ, թէ վարակուած անձերու թիւը մօտաւորապէս ինչպէ՞ս կը զարգանայ, երբ մահանալու հաւանականութիւնը փոքր է: «Քորոնա»-ի պարագային, այդ այսօրուան տուեալներով 3,7 տոկոս է: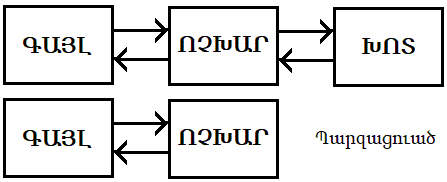

Վերի օրինակին մէջ բաժանումներու միջեւ փոխազդեցութիւն չկայ: Այլ օրինակ մը կարելի է վերցնել բնութենէն: Ենթադրենք, որ բնութիւնը կը բաղկանայ խոտէ (բուսականութիւն), ոչխարներէ (արածողներ) եւ գայլերէ (գիշատիչներ): Խոտի աճը կախեալ է կլիմայական պայմաններէ: Ենթադրենք, որ այդ պայմաններու փոփոխութիւնը դանդաղ է` բաղդատած անասուններու աճին: Այսինքն քանի մը տասնեակ տարի` բաղդատած քանի մը տարուան: Ոչխարներու աճի տոկոսը կը մնայ բնական: Բայց սպանութիւնը կախեալ է գայլերու թիւէն: Գայլերու աճը կախեալ է ոչ միայն իրենց թիւէն, այլ նաեւ` ոչխարի առատութենէն: Գիշատիչներ աւելի արագ կը ծննդաբերեն, երբ որսը առատ է: Այս յարաբերութիւնները կարելի 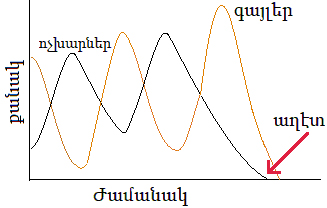է թուաբանականօրէն ձեւաւորել: Այդ կարելի է տեսնել դասագիրքերու մէջ: Իտէալ պայմաններու տակ կը գոյանայ կայուն կացութիւն: Անասուններու թիւը կը մնայ անփոփոխ: Երբ հաւասարակշռութիւնը խախտի, տեղի կ՛ունենան տատանումներ: Մեծ խախտում մը կրնայ աղէտալի հետեւանքներ ունենալ: Գծապատկերը ցոյց կու տայ, որ նախ սակաւաթիւ դարձած ոչխարները ի սպառ կը յօշոտուին բազմացած գայլերու կողմէ, եւ ապա սովահարութեան դատապարտուած գայլերը կ՛անհետանան:

Օրինակին ուսանելի կէտը այն է, որ քանակի մը փոփոխութիւնը կախեալ է այլ քանակէ մը: Համաճարակներու պարագային, առողջ մարդոց թիւի նուազումը կախեալ է վարակուած անձերու քանակէն, ինչպէս ողջ ոչխարներու թիւի նուազումը` գայլերու քանակէն: Մեծ խախտումներ կրնան յանգիլ աղէտի:

Ե-Վ-Ա Կաղապարում.- Գիտութեան օրէնքներու մէկ մեծ տոկոսը «տարբերական հաւասարութիւններ» (differential equations) են: Նիւթոնի հռչակաւոր «Երկրորդ օրէնքը», օրինակ, կ՛ըսէ, որ թափի (Momentum, P) փոփոխութիւնը (d/dt) հաւասար է գործադրուած ուժին (Force, F) (3): Կամ`  d/dt (P) = F:

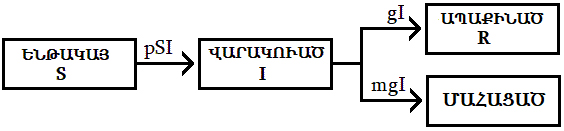
«Բաժանումային կաղապարումի» պարագային, մենք յստակօրէն գործ ունինք փոփոխութիւններու հետ, ուրեմն անհրաժեշտ է գործածել  «տարբերական հաւասարութիւններ»: Ներկայ ձեւաւորումը սկիզբ առած է 1927-ին: Կը վերագրուի գիտնականներ Ուիլիըմ Քերմաքի եւ Կրէյ ՄքՔենտրիքի, որոնք  աշխատած են Հնդկաստանի եւ Սուտանի բրիտանական գաղութներուն մէջ, ուր համաճարակներ պարբերաբար մեծ թիւով զոհեր կը խլէին (4):

Կաղապարումը կը ճանչցուի որպէս SIR  Susceptible-Infected-Recovered, որ կը թարգմանուի «Ենթակայ-Վարակուած-ապաքինած» (Ե-Վ-Ա): Թուաբանականօրէն մահացողներու թիւը կարելի է ներառել «ապաքինող»-ներու մէջ, թէեւ այդ չար կատակ կը թուի (5): Մահացողներու թիւը կախում ունի բժշկական խնամքէ եւ` ոչ միայն: Մեծապէս կը տարբերի երկրէ երկիր:

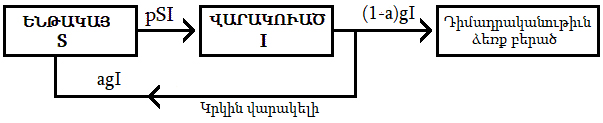Եթէ ոչ բոլոր ապաքինողները դիմադրականութիւն ձեռք կը բերեն, ապա անոնցմէ մէկ տոկոսը (a) կը վերադառնայ դէպի «Ենթակայ» բաժանում: Գիտնականներ կը նշեն, որ այդ հաւանականութիւնը, ցաւօք, առկայ է «Քորոնա»-ի պարագային:

Եթէ համաճարակը կարճատեւ է, կարելի է անտեսել բնակչութեան բնական աճը եւ ընդհանուր թիւը համարել անփոփոխ: Եթէ ընդհանուր թիւը անփոփոխ է, ապա կարիք չկայ ապաքինողներու թիւը նկատի ունենալ հաւասարութիւններու մէջ, որովհետեւ այդ կարելի է դիւրաւ հաշուել:

Եթէ ապաքինելու հաւանականութիւնը (g) է, ապաքինողներու թիւը կախում ունի այդ հաւանականութենէն եւ վարակուածներու քանակէն (I): Թուաբանութեան լեզուով`

d/dt (R) = gI

Վարակուելու պարագան քիչ մը աւելի բարդ է: Այդ կախում ունի թէ՛ վարակուած եւ թէ՛ վարակուելու ենթակայ անձերու քանակէն (I եւ S):  Կախում ունի ի հարկէ նաեւ վարակելու հաւանականութենէն (p): Եթէ մէկ վարակուած անձ մէկէ աւելի անձեր վարակէ, ապա տեղի կ՛ունենայ աճող համաճարակ: Վերջերս մեր ենթարկուած տնային կալանքը կը միտէր նուազեցնել այդ հաւանականութիւնը: Բարեբախտաբար «Քորոնա»-ն կը խնայէ մանուկները: Այսինքն ոչ ամբողջ բնակչութիւնը ենթակայ է վարակին: Քերմաք-ՄքՔենտրիք սրբագրուած  հաւասարութիւնները հետեւեալ ձեւով կ՛ամփոփեն վերի պատումը.

dS/dt=-pIS+ agI     (ա)
dI/dt=+pIS–gI       (բ)

Երկու հաւասարութիւն եւ երկու անյայտ, ուրեմն` լուծելի: Անոնք, որոնք բաւարար չափով ծանօթ են համարողութեան (Calculus), կրնան լուծումը տեսնել բազմաթիւ աղբիւրներու եւ դասագիրքերու մէջ (6):

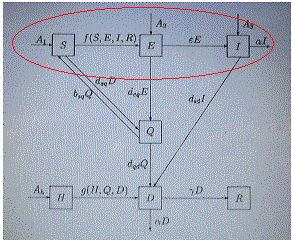Հաշուարկներ.- Հարկ է ի մտի ունենալ, որ վերի համեմատաբար գծանկարները եւ լուծելի հաւասարութիւնները ձեռք բերուած են ի գին մեծ պարզացումներու: Ընդարձակ տարածքներու բնակչութիւնը նկատուած է համանման: Անտեսուած են տարիքային ազդակները, ժահրի «թխսային» (incubation) տեւողութիւնը («Քորոնա»-ի պարագային, թերեւս` երկու շաբաթ) եւ այլն (7):  Բացի այդ, այստեղ կան լոկ երեք բաժանումներ եւ երկու հաւասարութիւն: Մասնագիտական ուսումնասիրութիւններ կ՛ունենան շատ աւելի մեծ թիւով բաժանումներ եւ հաւասարութիւններ: 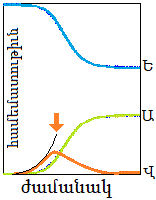Վերի պատկերը կողքի գծապատկերի լոկ վերի ընդգծուած մասն է: Հարցը այն է, որ նման հաշուարկներ գրահաշուային (analytic) ձեւով լուծելի չեն: Պատասխաններ կարելի է ստանալ միայն կէտ առ կէտ համակարգչային հաշուողական (computational) ձեւով, եթէ ի հարկէ կան հաւաստի տուեալներ: Իսկ Լիբանանի մէջ վիճակագրական տուեալները քաղաքականացուած են եւ խառնաշփոթ:

Կողքի գծապատկերը ցոյց կու տայ հնարովի  «տեսական» համաճարակ մը: Համեմատութիւնները մեծապէս չափազանցուած են, որպէսզի դիւրաւ տեսանելի ըլլան: Չափազանցուած պատկերին մէջ սլաքով նշուած է վարակուողներու սկզբնական աճի գծագիրը: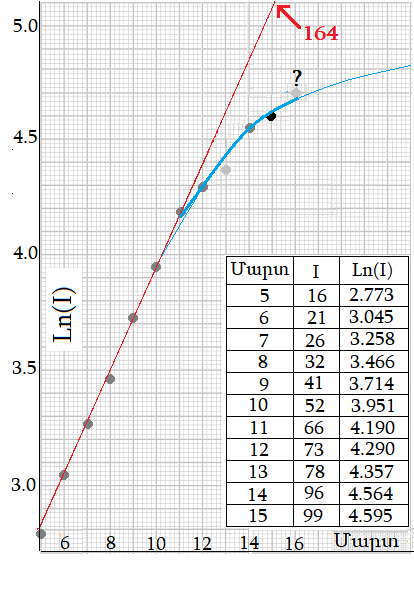

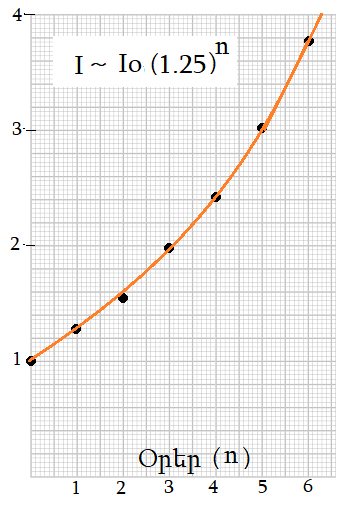
Նախատեսումներ.- Քերմաք-ՄքՔենտրիքի (բ) հաւասարութիւնը կը նախատեսէ, որ աճը ունենայ «երկրաչափական ընթացք» (geometric progression կամ exponential growth, որ թերեւս կը թարգմանուի «աստիճանացուցական աճ») (8): Ըստ այդ, հաւասար ժամանակամիջոցներու մէջ արձանագրուած աճը կըլլայ հաւասար: Լիբանանի պարագային, աճը օրական մօտ 25 առ հարիւր էր մինչեւ մարտ 11: Այս հարկ էր, որ ահազանգ համարուէր, որովհետեւ աղէտահար Իտալիոյ մէջ  մարտի 1-էն 11 միջոցին վարակի աճը եղած է 21 տոկոս (9): Կողքի գծապատկերի հրատարակումէն ետք, Իտալիոյ մէջ վարակուածներու թիւը հասած է շուրջ 21 հազարի: Այդ կը նշանակէ 69 տոկոսի աճ, որ կը համապատասխանէ օրական շուրջ 14 տոկոսի (10):

Սկզբնական ընթացքէն շեղումը կարելի կը դարձնէ հաշուարկել Քերմաք-ՄքՔենտրիք կաղապարումին մէջ տեսնուող (p), (a) եւ (g) քանակները, եւ նախատեսել, թէ ե՞րբ կրնայ սկսիլ վարակի տեղատուութիւնը: Այդ կարելի է կատարել այն հաստատութիւններու մէջ, ուր տրամադրելի են յարիր համակարգչային ծրագիրներ (package): Նման ծրագրեր պէտք է ներառեն նաեւ վիճակագրական տուեալներու մէջ գտնուող անորոշութիւնները (uncertainty):

Անհատական միջոցներով վարակի ընթացքը նախատեսելու համար կարելի է դիմել համեմատաբար դիւրաւ հաշուարկելի տիպարահամարային (logarithmic) գծապատկերներու: Եթէ տուեալները հաւաստի են, ապա աճի թափը սկսած է նուազիլ` սկսած մարտի 11-էն: Այժմ դեռ կանուխ է աներկբայ նախատեսութիւններ կատարելու համար: Բացի այդ, վերջին օրերու պաշտօնական տուեալները շփոթ կը ստեղծեն: Լրատուական միջոցներ այս մասին բողոքած են: Կացութիւնը լուրջ է: Այսուհանդերձ, կայ յոռետեսութիւնը մեղմելու տուեալ: Եթէ սկզբնական աճը անփոփոխ շարունակուէր, ապա վարակուողներու թիւը հարկ է որ մարտ 15-ին հասնէր 164-ի (տես Լիբանանի գծապատկերը): Մինչդեռ Կարմիր խաչի յայտարարած թիւը 99 է: Այդ սկզբնական աճի լոկ 60 տոկոսն է: Եթէ նոյնիսկ վաղը 10 կամ 15 նոր վարակ արձանագրուի, աճի թափը յստակօրէն կոտրուած է: Ճիշդ չէ սկզբնական աճի հիման վրայ ենթադրութիւններ կատարել:

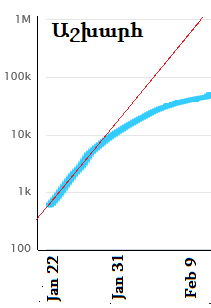Թերեւս պաշտօնական տուեալները ամբողջական չեն: Հաւանական է, որ կարգ մը կողմեր կը փորձեն պահել իսկական թիւերը: Անհաւանական է սակայն, որ կեղծ թիւերը այնպէս յօրինուէին, որ համապատասխանէին տեսականօրէն ճշգրիտ յարաբերութեան, որ կը տեսնենք վերեւի գծապատկերներուն մէջ: Այդ պատրաստի դաւադրական տեսութիւն է (conspiracy theory), որ անօգուտ կը գտնեմ: Հաւանական է որ  աճի զգալի նուազումը առ նուազն մասամբ հետեւանք է քաղաքացիներու կամովի տնային կալանքին: Բացի այդ, Լիբանանի մէջ վարակի ընթացքը նման է համաշխարհային մակարդակի վրայ արձանագրուած աճի ընթացքին: Եթէ սկզբնական թափը պահպանուէր, ապա հարկ էր որ փետրուար 9-ին վարակուողներու թիւը հասնէր մէկ միլիոնի: Մինչդեռ իսկական թիւը շուրջ 36 հազար էր:

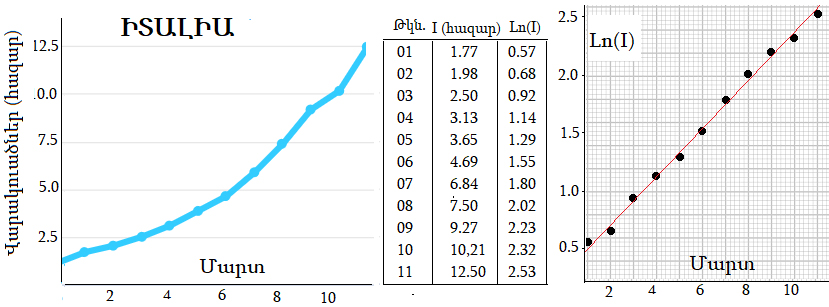
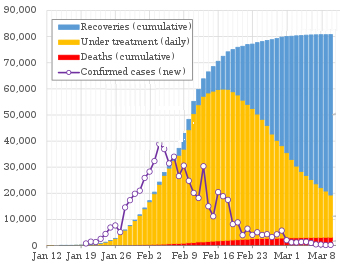Կողքի գծապատկերը ցոյց կու տայ վարակի ընթացքը Չինաստանի մէջ: Նախ նկատել, թէ իսկական վիճակագրական պատկերը որքան նման է տեսականին: Ապա նկատել, որ վարակուողներու թիւը արդէն իսկ սկսած էր նուազիլ փետրուար 16-ին: Այժմ այդ նոր զոհերու թիւը համեմատաբար աննշան է:

Չինաստանի օրինակը ցոյց կու տայ, որ ժահրը, այո՛, արագ կը տարածուի, բայց յաղթահարելի է: Յոռետեսութիւնը անկարողութեան զգացումի, ճակատագրապաշտութեան ուրեմն եւ անփութութեան կը մղէ: Ա՛յդ է, որ վստահաբար կը յանգի աղէտի:

15 մարտ 2020

1.- Calculus-ի գիւտը կը վերագրուի Նիւթոնի բայց այս մասին կայ բանավէճ: Նիւթոն բացառիկ հանճար մըն էր որ միաժամանակ ունէր նկարագրի բազմաթիւ յոռի գիծեր: Անոնցմէ մէկն էր գաղափարներու գողութիւնը:

2.- Պերնուլլի ընտանիքը այդ շրջանին տուած է առ նուազն հինգ ականաւոր գիտնականներ: Հեղուկագիտութիւնը առնչուած է իմ 2-րդ եւ 3-րդ աւարտաճառերուս:

3.- Երբ զանգուածը (M) անփոփոխ է, այդ օրէնքը կը վերածուի դասագրքային ձեւին`  Mdv/dt = F. Հանճարեղ Նիւթոն առաջադրած էր ճշգրիտ ընդհանուր ձեւը.- d(Mv)/dt = F.

4.- Տես https://royalsocietypublishing.org/doi/10.1098/rspa.1927.0118.

5.- Եթէ բաղդատած ապաքինողներու, մահացողներու համեմատութիւնը (m) ծանօթ է, ապա կարիք չկայ առանձին բաժանում յատկացնելու անոնց: gI + mgI = ([1+m]g)I = g’I   g’ =  [1+m]g: Քորոնայի պարագային Չինաստանի մէջ այդ կը նշանակէ մօտ 3,5 տոկոս «ճշդում»: g’ =  1.035g.

6.- G Shabbiret al “A note on Exact solution of SIR and SIS epidemic models”, Math CA 2010.

7.- Westreich D (ed.), “Trends in the Mechanistic and Dynamic Modeling of Infectious Diseases”,  Epidemiologic Methods, July 2016.

8.- Համաճարակի սկզբնաւորութեան ենթականերու թիւը գրեթէ հաւասար է ընդհանուր թիւին  S – N   իսկ վարակուողներու թիւը գրեթէ զերօ է  I – 0: dI/dt = pIS – gI հաւասարութիւնը կը պարզանայ dI/dt = pNI  կամ  dI/I = (pN)dt: Այսինքն հաւասար ժամանակամիջոցներու մէջ աճը հաւասար է: Լիբանանի պարագային այդ աճը օրական մօտ 25 առ հարիւր էր մինչեւ մարտ 11:

9.- Տարբերութիւնը աննշան կը թուի, բայց երեք շաբթուայ ընթացքին Լիբանանի աճը պիտի ըլլայ Իտալիոյ մօտ կրկինը ((1.25/1.21)^21 = 1.98: Այսինքն մօտաւորապէս կրկին:

10,- Անոնք որ ծանօթ են «բարդ տոկոս»-ի (compound interest) հաշուարկին պիտի հասկնան թէ (1 + 14%)^4 = 1 + 69% եւ ոչ 1+56%: Լիբանանի հոյաճ պարտամուրհակները վկայ: